
GEOINFORMATICS RESEARCH PAPERS, publ. BS1001, doi:10.2205/2013BS008, 2013
A. A. Lushnikov1,2, A. D. Gvishiani1, Yu. S. Lyubovtseva1, A. A. Makosko3
1Geophysical Center of Russian Academy of Sciences, Moscow, Russia
2Karpov Institute of Physical Chemistry, Moscow, Russia
3Obukhov Institute of Atmospheric Physics, Moscow, Russia
.This paper suggests a collection of demographic models describing the time evolution of the medico-demographic indicators of population: population size, population age distributions, fertility, mortality etc. The evolution of the population is considered to be driven by birth–death processes and deceases. For each model a respective set of evolution equation is formulated. These equations include kinetic parameters that have the meaning of the transition rates and whose values are linked to the characteristics of current medico-demographic state. We consider a number of evolution demographic models of different levels the lowest of which includes uni-gender population, where, in addition, newborns appear irrespective of the population distribution over ages. Then we introduce more sophisticated models that distinguish the ages of the members of community and their gender. We also consider the situations, where infections and deceases affect the medico-demographic state and thus the evolution of the population. The results of our study are illustrated by some numerical examples.
Demographic statistics operates with a range of concepts that, from the first sight, seem very natural. Among them the death rate, birth rate, life span, morbidity, etc.. Each of these characteristics is attributed to a well-measured quantitative demographic indicators, e.g., the number of deaths per thousand of the population or the average age equal to the total age of a group of people divided by the number of people in the group. Such indicators are widely used in medical statistics as well as in many other social Sciences. These indicators are compared, and on the basis of such comparison the conclusions can be drawn on the reasons of this or that social phenomenon [Alho and Spencer, 2005; Bongaarts and Bulatao, 2000; McVean, 2003; Medkov, 2005; Preston et al., 2001; Schoen, 2007; Venetskii, 1981].
Demographic studies based on certain reasonable assumptions are, undoubtedly, the valuable tools for providing the information about the future size and structure of the population. Current demographic trends, characterized by low fertility and increasing longevity, lead to an ageing population that has definite and unpleasant economic and budgetary implications. Next, ethno-cultural diversity, changing patterns in partnership behaviors and household formation, confront our society with complex challenges. [Clark, 1976; Getz and Haight, 1989; Hastings, 2000; Lutz, 2001].
One of the most significant conditions in carrying out accurate population estimates, especially in a context of strong instability of demographic evolution, is the availability of the statistical information about the most recent evolution of demographic phenomena. Meanwhile, all these phenomena are governed by some laws and thus can be described with the help of adequately formulated mathematical models [Charlesworth, 1980; Fowler, 1977; Hoppenstadt, 1975; Reinshaw, 1991; Webb, 1985]
There exist numerous attempts of mathematical description of the demographic situations, beginning with the classical work of Maltus who assuming the linear dependence of the birth–death process derived the well-known Maltus' exponential law. According to the Maltus law the population either unlimitedly grows or diminishes exponentially with time, depending on the ratio of birth-to-death rates. At the birth–death ratio equal to unity the population should not change, but this equilibrium occurs to be unstable. Moreover, the dependencies of the rate of both these processes on the population size can be principally different, so the position of the stationary point may depend on the population size.
The main goal of this paper is threefold:
The remainder of this paper is organized as follows. Next Section describes the basic principles underlying the demographic models and introduces to a couple of well known models: the simplest Maltus model linear with respect to the population number and the logistic model that takes into account some limitations put on the fertility rate. These limitations are related to the deficiency of resources, which prevents the families to grow (or lead to the growth of the mortality rate). In this Section we also consider a generalized logistic model, whose parameters depend on time and the nonlinearity introduced by the limitations is arbitrary (rather than quadratic, as in the classical logistic model). In Section 3 the distributions of population over the ages is introduced explicitly. In addition, we introduce the fertility active age groups, which leads to some additional and very serious complications. The evolution equation in this case becomes integro-differential. Still it is analyzable for linear evolution models. A simplified three age groups model ends up this Section. Section 4 extends the demographic models by introducing two genders, which simply doubles the number of demographic equations. For considering deceases and infections we introduce a model, where the demography of the decease carrier is taking into account (Section 5). The migration processes are considered in Section 6. We consider several settlements and formulate the demographic equation for each. The settlements are linked by the migration fluxes. In Section 7 we connect the parameters of the demographic models with the geomedical indicators. The concluding Section 8 summarizes the results of this paper.
In this Section we describe the basic principles of constructing the demographic models. There exists a lot of demographic models, but the principles of their formulation remain identical [Hastings, 2000; Hoppenstadt, 1975; McVean, 2003; Murray, 2002; Venetskii, 1981].
Let us consider an isolated settlement populated with a group of people. Let $n(t)$ be the number of people in the group at the moment of time $t$ (the average population size). We assume for simplicity that only two processes govern the time evolution of the population: the birth and the death. The population grows up due to the birth of new individuals and drops down due to their death. Then we can write down the following simple evolution equation,
\begin{eqnarray*} \frac{dn}{dt}= \varkappa f(n)-\lambda g(n)+I_++I_-. \end{eqnarray*}Here $\varkappa f(n)$ is the birth rate (the fertility rate) and $\lambda g(n)$ is the death rate (the mortality rate). The constants $\varkappa$ and $\lambda$ are referred to as the rate constants of the respective processes. The functions $f(n)$ and $g(n)$ describe the $n$-dependence of the rates of the birth and the death processes. The last two terms on the right-hand side (RHS) of this equation are the migration in- and outflows.
The simplest option is $f(n)=n$, $g(n)=n$, i.e., the birth and the death rates are linear in the population size $n(t)$. We thus come to the simple linear differential equation,
\begin{eqnarray*} \frac{dn}{dt}=\varkappa n-\lambda n. \end{eqnarray*}The solution to this equation is well known,
\begin{eqnarray*} n(t)=n_0e^{\mu t}. \end{eqnarray*}This exponential dependence is referred to as the Maltus law. Here and below
\begin{eqnarray*} \mu=\varkappa-\lambda \qquad{\rm and}\qquad n_0=n(0). \end{eqnarray*} |
| Figure 1 |
It is seen that the population is either grows up if the fertility exceeds mortality ($\mu>0$) or drops down otherwise (see Figure 1).
The Maltus model does not take into account the nonlinearity related to limited resources for the development of the self-sustainable population. This resource factor is introduced in the standard logistic model by a multiplier in the expression for the fertility rate: namely, the term $\varkappa n$ is replaced by $\varkappa n(1-\alpha n)$. The last multiplier in this expression diminishes the total fertility rate. The coefficient $\alpha$ is an empirical constant that should be determined from current demographic data. For example, $\alpha$ can be equal to $1/n_{\max}$, where $n_{\max}$ is the maximal possible size of the offspring limited, let us say, with the total existing living area or the total food resource. Hence, the logistic model is formulated as
\begin{eqnarray*} \frac{dn}{dt}=\varkappa n(1-\alpha n)-\lambda n. \end{eqnarray*}The solution to this equation is known. At $\mu>0$
\begin{equation} \tag*{(1)}\label{1} n(t)=\frac{ n_0}{s(1-e^{-\mu t})+e^{-\mu t}}. \end{equation}Here $s=\alpha\varkappa n_0/\mu$ is the dimensionless parameter governing the evolution process. If $s=1$ (or $n_0=\mu/\varkappa\alpha$) the population does not change. Moreover, $n(t)\longrightarrow\mu/\varkappa\alpha$ as $t\longrightarrow\infty$.
At negative $\mu$ the logistic curve is different,
\begin{equation} \tag*{(2)}\label{2} n(t)=\frac{ n_0e^{-|\mu| t}}{s(1-e^{-|\mu| t})+1}. \end{equation}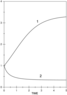 |
| Figure 2 |
 |
| Figure 3 |
Respective curves given by Eqs. (1) and (2) are shown in Figure 2 and Figure 3.
The logistic model is seen to belong to the class of models describing by the equation, (the generalized logistic model),
\begin{equation} \tag*{(3)}\label{3} \frac{dn}{dt}= a n^\sigma-b n. \end{equation}The coefficients $a$ and $b$ can have any sign. Moreover, they depend on time. On introducing $n(t)=m(t)e^{-B(t)}$ with $B(t)=\int_0^tb(t')dt'$ yields,
\begin{equation} \tag*{(4)}\label{4} \frac{dm}{dt}=ae^{-(\sigma-1)B(t)}m^\sigma. \end{equation}The substitution $\tau=\int_0^ta(t')e^{-(\sigma-1)B(t')}dt'$ reduces Eq. (4) to
\begin{eqnarray*} \frac{dm}{d\tau}= m^\sigma. \end{eqnarray*}This equation with the initial condition $m(0)=n_0$ is readily solved. The solution at $\sigma>1$ is,
\begin{equation} \tag*{(5)}\label{5} m(\tau)=\left[\frac{n_0^{\sigma-1}}{1-(\sigma-1)\tau n_0^{\sigma-1}} \right]^{\frac1{\sigma-1}}. \end{equation}At $\sigma<1$
\begin{equation} \tag*{(6)}\label{6} m(\tau)=[(1-\sigma)\tau +n_0^{1-\sigma}]^{\frac1{1-\sigma}}. \end{equation}Until this moment our consideration did not include the age distribution inside the population group. Now we correct this deficiency. To this end we introduce $n(a, t)$ – the number of individuals whose age lies within the interval $[a,a+da]$ [Charlesworth, 1980].
We first assume that nothing happens to the individuals except for the changes in their age. Of course, the age depends on time but, in general, it does not coincide with current time (so-called "physiological age"). The function $f (t) = n (a (t), t)$, in accordance with our assumption that nothing happens to the population, does not change with time, i.e., it satisfies the equation,
\begin{eqnarray*} \frac{df}{dt}=0 \end{eqnarray*}or
\begin{equation} \tag*{(7)}\label{7} \frac{\partial n}{\partial t}+\dot a\frac{\partial{n}}{\partial{a}}=0. \end{equation}Here $\dot a$ stands for the rate of change of age with time. It is usually assumed that $\dot a=1$, i.e., the age of the individual simply coincides with the time elapsed since its birth. Then Eq. (7)) takes the form:
\begin{eqnarray*} \frac{\partial n}{\partial t}+\frac{\partial n}{\partial a}=0. \end{eqnarray*}This is a first-order partial differential equation, the general solution to which is,
\begin{eqnarray*} n (a, t) = n_0 (a - t), \end{eqnarray*}where $n_0 (a) = n (a, 0)$ is an arbitrary function of a single argument the form of which is determined by the initial conditions. (the age distribution at the initial moment of time $t = 0$).
Now we consider a more complicated and quite realistic example. Let the initial age distribution of population be $n_0(a)$. Next, the individuals are assumed to die, but no one is born. The rate of mortality $\lambda=\lambda(a)$ depends on the age. Then instead of Eq. (7) we have to solve the equation,
\begin{equation} \tag*{(8)}\label{8} \frac{\partial n}{\partial t}+\frac{\partial n}{\partial a}=-\lambda(a)n. \end{equation}The solution to this equation is:
\begin{equation} \tag*{(9)}\label{9} n(a,t)=\theta(a-t)n_0(a-t)\exp[-\int\limits_0^a\lambda(a')da']. \end{equation}Here $\theta(x)$ is the Heaviside step-function equal to unity for positive $x$ and zero otherwise. Its presence means that there are no individuals of negative age.
Now we add to Eq. (8) the term responsible for fertility. The evolution equation acquires the form:
\begin{equation} \tag*{(10)}\label{10} \frac{\partial n}{\partial t}+\frac{\partial n}{\partial a}=\varkappa N(t)\delta(a)-\lambda(a)n , \end{equation}where $\varkappa$ is the fertility rate, $ N (t)$ is the number of pairs able to give offspring, and the delta-function corresponds to the fact that the age of newborns is zero. We assume that
\begin{equation} \tag*{(11)}\label{11} N(t)=\left[\int\limits_0^\infty S(a)n(a,t)da \right]^s. \end{equation}Here the form-factor $S (a)$ is responsible for the contribution of the age group in the population reproduction rate. The function $S(a)$ is normalized to unity, i.e.,
\begin{eqnarray*} \int\limits_0^\infty S(a)da=1. \end{eqnarray*}The stationary distribution over ages meets the equation,
\begin{equation} \tag*{(12)}\label{12} \frac{dn_s}{da}=\varkappa N_s\delta(a)-\lambda(a)n_s. \end{equation}Here index $s$ corresponds to the stationary limit. On solving Eq. (12) yields,
\begin{equation} \tag*{(13)}\label{13} n_s=\varkappa N_s\exp[-\Lambda(a)]\theta(a), \end{equation}where $\Lambda(a)=\int_0^a\lambda(a')da'$. Now we have to find $N_s$. Using the definition (11), we find
\begin{eqnarray*} N_s=\left[\varkappa\int\limits_0^\infty S(a')\exp[-\Lambda(a')da'] \right]^{-(s-1)}. \end{eqnarray*}If $s=1$ (linear case) we cannot find $N_s$ not solving the time dependent problem.
The total number of individuals in the population is,
\begin{equation} \tag*{(14)}\label{14} N=\varkappa N_s\int\limits_0^\infty \exp[-\Lambda(a')]da'. \end{equation} |
| Figure 4 |
The result is seen to be independent of the initial stage of the population development. Figure 4 displays the age distribution for the stationary case.
In this Subsection we analyze the solution of the birth–death equation (10). We start with a given initial distribution over ages $n_0(a)$ and seek for a solution as a sum of the general solution to the homogeneous equation (without the first term on its right-hand side) and a particular solution to the inhomogeneous one. The general solution to the homogeneous equation is already known. It is given by Eq. (9). The particular solution to the inhomogeneous equation is easy to construct. Finally, we find,
\begin{eqnarray*} n(a,t)=[n_0(a-t)\theta(t-a)+ \end{eqnarray*} \begin{equation} \tag*{(15)}\label{15} \varkappa N(t-a)\theta(a)\theta(a-t)]\exp[-\int_0^a\lambda(a')da']. \end{equation}At long times we obtain the stationary solution Eq. (13). The general solution Eq. (15) consists of two parts: a running wave corresponding to the initial distribution of ages and a wave related to the birth process. The first part entirely dies out with time. The second wave after a transient period of time converts to the stationary regime Eq. (13).
The problem is not yet completely solved, for we did not find $N (t)$. In order to find this function let us introduce $I (t) = N^{1/s}$, so that $N (t) = I^s (t)$. For $I (t)$ we formulate a nonlinear integral equation, which immediately follows from Eq. (15) after multiplying its both sides by $S (a)$ and integrating over $a$ from zero to infinity.
\begin{eqnarray*} I(t)=\varkappa\int_0^tI^s(t-a)S(a)e^{-\Lambda(a)}da+ \end{eqnarray*} \begin{equation} \tag*{(16)}\label{16} \int\limits_t^\infty n_0(a-t)S(a)e^{-\Lambda(a)}da. \end{equation}The last term on the RHS of this equation is a known function of time. Now everything is clear. It is sufficient to solve Eq. (16), and to draw conclusions on the impact of various factors on the evolution of the population from Eq. (14).
We complete this Section by one small improvement. We redefine the $I (t)$ in such a way that to take into account the finiteness of the pregnancy period $t_0$. The result is evident,
\begin{eqnarray*} I(t)=\int\limits_0^\infty n(a,t-t_0)S(a)da. \end{eqnarray*}Here $t_0$ is the period of pregnancy.
It is possible to simplify the above consideration by introducing the following approximation: All population is divided into three groups
The meaning of this model is absolutely transparent and does not need in additional explanations. The respective mathematical model is also readily derived from Eq. (10) on integrating the latter from $a_{k-1}$ to $a_k$ and assuming the mortality to be constant within the given age group. These equations are,
\begin{eqnarray*} \frac{dn_1}{dt}=\gamma\varkappa n_2- n_1-\lambda_1n_1, \end{eqnarray*} \begin{eqnarray*} \frac{dn_2}{dt}= n_1- n_2-\lambda_2 n_2, \end{eqnarray*} \begin{eqnarray*} \frac{dn_3}{dt}= n_2-\lambda_3 n_3. \end{eqnarray*}Here $\gamma$ is the breeding coefficient (the number of babies produced by one mother) and $\lambda_i$ is the mortality within the respective group. This is the linear version of the three-age model. The nonlinearities can also be introduced.
Now we extend our consideration to the case, where the reproduction demands two individuals of opposite sex. We thus introduce two age distributions: $m (a, t)$ and $f (a, t)$ for the individuals of masculine and feminine genders respectively. These two functions meet the system of equations,
\begin{eqnarray*} \frac{\partial m}{\partial t}+\frac{\partial m}{\partial a}=\varkappa_mI_mI_f\delta(a)-\lambda_m(a)m, \end{eqnarray*} \begin{eqnarray*} \frac{\partial f}{\partial t}+\frac{\partial f}{\partial a}=\varkappa_fI_mI_f\delta(a)-\lambda_f(a)f. \end{eqnarray*}Here
\begin{eqnarray*} I_m(t)=\int\limits_0^\infty S_m(a)m(a,t-t_0)da, \end{eqnarray*} \begin{eqnarray*} I_f(t)=\int\limits_0^\infty S_f(a)f(a,t-t_0)da. \end{eqnarray*}Constants $\varkappa$ and $\lambda(a)$ with the corresponding indices have the same meaning as above, i.e., they are the birth–death rates constants for men and women respectively.
Again, as above we get the following set of equations for $I_m(t)$ and $I_f(t)$:
\begin{eqnarray*} I_m(t)=\varkappa_m\int\limits_0^tI_m(t-a)I_f(t-a)S_m(a)e^{-\Lambda_m(a)}da+ \end{eqnarray*} \begin{eqnarray*} \int\limits_t^\infty n_{0m}(t-a)I_f(t-a)S_m(a)e^{-\Lambda_m(a)}da, \end{eqnarray*} \begin{eqnarray*} I_f(t)=\varkappa_f\int\limits_0^tI_m(t-a)I_f(t-a)S_f(a)e^{-\Lambda_f(a)}da+ \end{eqnarray*} \begin{eqnarray*} \int\limits_t^\infty n_{0f}(t-a)I_f(t-a)S_f(a)e^{-\Lambda_f(a)}da. \end{eqnarray*}Let us assume that the female population limits the rate of reproduction. This is especially typical for hen-houses, where one cock is able to provide all the offspring of chickens. In the human community the birth rate is limited by the capacity of the female body rather than the population of men. Indeed, if there are many men, and only one woman, the number of children she may have does not depend on the size of the male population.
So, if the fertility is limited by the population of women, we can rewrite the birth–death equation for women in the form:
\begin{eqnarray*} \frac{\partial f}{\partial t}+\frac{\partial f}{\partial a}=\varkappa_fI_f\delta(a)-\lambda_f(a)f. \end{eqnarray*}The birth–death process for men is also limited by the number of women,
\begin{eqnarray*} \frac{\partial m}{\partial t}+\frac{\partial m}{\partial a}=\varkappa_mI_f\delta(a)-\lambda_m(a)m. \end{eqnarray*}For the fertility of women $I_f(t)$ we have:
\begin{eqnarray*} I_f(t)=\int\limits_0^\infty S_f(a)f(a,t-t_0)da. \end{eqnarray*}The integral equation for $I_f(t)$ has the form:
\begin{eqnarray*} I_f(t)=\varkappa_f\int\limits_0^t I_f(t-a) S_f(a)e^{-\Lambda_f(a)}da+ \end{eqnarray*} \begin{equation} \tag*{(17)}\label{17} \int\limits_t^\infty n_{0f}(a-t) S_f(a)e^{-\Lambda_f(a)}da. \end{equation}The last term on the RHS of Eq. (17) is a known function of time. Hence, Eq. (17) can be solved by using the Laplace transform. We introduce
\begin{eqnarray*} I_f(p)=\int\limits_0^\infty I_f(t)e^{-pt}dt, \end{eqnarray*} \begin{eqnarray*} S_f(p)= \int\limits_0^\infty S_f(a)e^{-\Lambda_f(t)}e^{-pt}dt \end{eqnarray*}and
\begin{eqnarray*} Q_f(p)=\int\limits_0^\infty e^{-pt}\int\limits_t^\infty n_{0f}(a-t)S_f(a)e^{-\Lambda_f(a)}dadt. \end{eqnarray*}From Eq. (17) we finally get,
\begin{eqnarray*} I_f(p)=\frac{Q_f(p)}{1-\varkappa_fS_f(p)}. \end{eqnarray*}Let $S_f(a)$ be the gamma-distribution,
\begin{eqnarray*} S_f(a)=a^re^{-ra} \end{eqnarray*}and $\Lambda(a)=\lambda a$. Then
\begin{eqnarray*} S_f(p)=\frac{r!}{(p+r+\lambda)^{r+1}}. \end{eqnarray*}For $n=0$ we have:
\begin{eqnarray*} I_f(p)=Q_f(p)+\varkappa_f\frac{Q_f(p)}{p+r+\lambda-\varkappa_f}. \end{eqnarray*}Accordingly, the
\begin{eqnarray*} I_f(t)=\int\limits_t^\infty n_{0f}(t-a)S_f(a)e^{-\Lambda_f(a)}da+ \end{eqnarray*} \begin{eqnarray*} \int\limits e^{-(\varkappa-\lambda-r)(t-\tau)} \int\limits_\tau^\infty n_0f(a-\tau)S(a)dad\tau. \end{eqnarray*}In the same spirit we can write down the formulas for $r>0$.
This Section demonstrates how to introduce the deceases to the above described schemes. For simplicity we consider the population comprising $x(t)$ healthy and $y(t)$ ill individuals. We also assume that the fertility and the mortality are linear with respect to the population numbers and that the members of $y$ group never recover (irreversible deceases).
According to our assumptions the simplest possible set of equation looks as follows:
\begin{equation} \tag*{(18)}\label{18} \frac{ dx}{dt}=\varkappa x-\mu x-\lambda_hx. \end{equation}The RHS of this equation claims that the healthy people appear with the rate $\varkappa x$, they get ill with the rate $\mu x$, and die with the rate $\lambda_h x$. The second equation describes the dynamics of $y$-group,
\begin{equation} \tag*{(19)}\label{19} \frac{ dy}{dt}=\mu x-\lambda_iy. \end{equation}Now the first term on the RHS of this equation describes the morbidity rate. It enters the equation with the positive sign. The second term is the mortality rate. We assume that the ill people die faster than the healthy ones, i.e., $\lambda_i>\lambda_h$. One sees that Eqs. (18) and (19) are a modification of the Maltus model.
The solution to Eqs. (18) and (19) is,
\begin{eqnarray*} x(t)=\frac{\varkappa n_0}{\varkappa-\lambda_h-\mu}e^{(\varkappa-\lambda_h-\mu)t}, \end{eqnarray*} \begin{eqnarray*} y(t)=\frac{\varkappa(\mu-\lambda_i) n_0}{(\varkappa-\lambda_h-\mu)^2}(e^{(\varkappa-\lambda_h-\mu)t}-e^{(\mu- \lambda_i)t}). \end{eqnarray*}Let us introduce the nonlinearity term to the set Eqs. (18) and (19).
\begin{equation} \tag*{(20)}\label{20} \frac{ dx}{dt}=\varkappa x^\gamma-\mu x-\lambda_hx. \end{equation}The RHS of this equation claims that the healthy people appear with the rate $\varkappa x^\gamma$, they catch a decease with the rate $\mu x$, and die with the rate $\lambda_h x$. The second equation describes the dynamics of $y$-group,
\begin{equation} \tag*{(21)}\label{21} \frac{ dy}{dt}=\mu x-\lambda_iy. \end{equation}Because the first equation of this set Eq. (20) is solved independently of the second Eq. (21), this set admits the analytical solution. Equations (5) and (6) yield the solution of the problem.
Let us return to our x–y model, but now we consider the morbidity rate proportional to $y$ – the number of already infected individuals. Next, the proportionality coefficient is assumed to depend on the population $Z$ of bacteria causing the decease.
\begin{equation} \tag*{(22)}\label{22} \frac{dx}{dt}=\varkappa x-\alpha(Z) xy +\beta y-\lambda_h x. \end{equation}This equation states that people are born (the first term on its RHS), get ill (the second term, proportional to the number of infected persons), recover with the rate $\beta$ (the third term) and die (the last term). The development of the ill population is given by the equation,
\begin{equation} \tag*{(23)}\label{23} \frac{dy}{dt}=\alpha(Z) xy -\beta y-\lambda_i y. \end{equation}The number of ill individuals grows because they infect the healthy ones (the first term on the RHS), some patients recover (the second term), and some die (the last term).
Finally, the population of bacteria grows proportionally to the total number of individuals, and the current population of bacteria. The respective birth–death equation is,
\begin{equation} \tag*{(24)}\label{24} \frac{dZ}{dt}=B(x+y)Z-\Lambda Z. \end{equation}Here $B$ is the breeding rate coefficient of the bacteria and $\Lambda$ is their death constant.
We note a useful equation:
\begin{eqnarray*} \frac{dN}{dt}=\varkappa x-\mu y-\lambda_h x \end{eqnarray*}i.e., the size of the population $N=x+y$ increases due to the production of new individuals and decreases by their death.
First, consider the case, where $\beta$ does not depend on the size of the population of microbes. Then the system of Eqs. (22) and (23) can be solved independently of Eq. (24). Let us find the stationary solution. It's easy to do. The result is,
\begin{eqnarray*} x_0=\frac{\beta+\mu}\alpha\, \qquad y_0=\frac{(\beta+\mu)(\varkappa-\lambda)}{\alpha^2}. \end{eqnarray*}There is another steady-state solution
\begin{eqnarray*} x_1=\varkappa/\lambda,\qquad y_1=0. \end{eqnarray*}This result corresponds to the complete absence of infected individuals.
Here we consider the simplest possible model that allows one to include the migration processes. We consider $N$ settlements and introduce $n_k(t)$ – the population size of the $k$-th settlement. We assume that the evolution of the populations is governed by the birth–death processes and the migration. The set of the evolution equations now looks as follows:
\begin{equation} \tag*{(25)}\label{25} \frac{dn_k}{dt}=[f(n_k)\varkappa_k-\lambda_kg(n_k)]+\sum\limits_{l\neq k}\mu_{k,l} n_l-n_k\sum\limits_{l\neq k}\mu_{l,k}. \end{equation}The meaning of the last two terms on the right-hand side of this equation is as follows. The third term describes the population influx to the $k$-th settlement due to migration of the population from all other settlements. The fourth term is the migration outflux from the $k$-th settlement to all others. The first two terms on the RHS of Eq. (25) are responsible for the birth–death processes. All the migration processes are assumed to be linear in the population numbers $n_k$. In principle, the migration processes can also include the nonlinearities appearing, e.g., due to the deficiency of working places.
The migration coefficients $\mu_{l,k}$ should be found from the regular measurements of the migration in- and outfluxes. It is important to note that $\mu_{i,k}\neq\mu_{k,i}$.
Above consideration of the simplest demographic models shows that the time dependence of the population size is determined by the dimensionless time $\mu t$ and the dimensionless group,
\begin{eqnarray*} s=\frac{\varkappa\alpha n_0^\sigma}\mu. \end{eqnarray*}Evolution equation (3) for the reduced population size $\nu=n/n_0$ and constant $a=\varkappa\alpha$ and $b=\mu$ can be rewritten in the dimensionless form:
\begin{eqnarray*} \frac{d\nu}{d\tau}= -s \nu^\sigma- \nu. \end{eqnarray*}Hence,
\begin{eqnarray*} n(t)=n_0\nu(\mu t,s). \end{eqnarray*}In what follows the absolute value of the dimensionless group $s$ is referred to as the demographic parameter. The condition $s=1$ defines the "equilibrium population size"
\begin{eqnarray*} n_0=\left(\frac\mu{\alpha\varkappa} \right)^{\frac1\sigma}. \end{eqnarray*}Now we show how to express the standard medico-demographic exponents in terms of the constants entering the birth–death equations of our demographic models.
The total number of men and women in a given social group is,
\begin{eqnarray*} N_m=\int\limits_0^\infty n_m(a,t)da, \qquad N_f=\int\limits_0^\infty n_f(a,t)da. \end{eqnarray*}The total size of the population is the sum of these two values,
\begin{eqnarray*} N (t) = N_m (t) + N_f (t). \end{eqnarray*}Fertility is the number of births per unit time per one person
\begin{eqnarray*} F(t)=\frac{\varkappa I_m(t)I_f(t)}{N(t)}. \end{eqnarray*}The number of births during time $T$ (say, one year)
\begin{eqnarray*} F_T(t)=\varkappa\int\limits_0^T \frac{ I_m(t)I_f(t)}{N(t)}dt. \end{eqnarray*}Extinction rate
\begin{eqnarray*} D_s(t)=\int\limits_0^\infty \lambda_s(a)n_s(a,t)da, \end{eqnarray*}where $s = f, m$. Mortality (number of deaths during time $T$)
\begin{eqnarray*} D_{sT}=\int\limits_0^Tdt\int\limits_0^\infty \lambda_s(a)n_s(a,t)da. \end{eqnarray*} |
| Figure 5 |
 |
| Figure 6 |
Figure 5 and Figure 6 demonstrate the application of the demographic modelling to the data on evolution of the population size in Russia before and after the changes happened at the end of 1990. The population growth before 1990 follows the classic Maltus law. The subsequent decline in the population size is evidently attributed to worsening the living conditions in Russia.
In this Section we resume the results of this paper.
We have formulated a collection of demographic models. The main idea of this study is to show that the demographic indicators are expressed in terms of the constants entering the demographic birth–death equations. In their turn, these constants having very close meaning and very close sounding enter to the standard medico-demographic indicators in rather complicate manners. On the other hand, the physical meaning of these constants is much more transparent and they are universal in contrast to the standard indicators. The main results of this paper may be summarized as follows
\acknowledgement{This research was funded by the Ministry of Education and Science of RF under Grant No. 14.515.11.0012.}
Alho, J. M., and B. D. Spencer (2005), Statistical Demography and Forecasting, Springer–Verlag, New York, 440.
Bongaarts, J., and R. Bulatao (Eds.) (2000), Beyond Six Billion. Forecasting the World's Population, National Academy Press, Washington D.C.
Charlesworth, B. (1980), Evolution in Age-Structured Populations, Cambridge University Press, Cambridge.
Clark, C. W. (1976), Mathematical Bioeconomics, the Optimal Control of Renewable Resources, John Wiley, New York.
Fowler, A. C. (1977), Mathematical Models in the Applied Sciences, Cambridge University Press, Cambridge.
Getz, W. M., and R. G. Haight (1989), Population Harvesting Demographic Models of Fish, Forests, and Animal Resources, Princeton University Press, Princeton, NJ.
Hastings, A. (2000), Population Biology, Springer–Verlag, New York.
Hoppenstadt, F. C. (1975), Mathematical Theories of Populations: Demographics, Genetics and Epidemics, volume 20 of CBMS lectures, SIAM Publications, Philadelphia.
Lutz, Wolfgang, Warren Sanderson and Sergei Scherbov (2001), The end of world population growth, Nature, 412, 543–545, doi:10.1038/35087589.
McVean, Gil (2003), Demographic Models, University of Oxford, Oxford, UK.
Medkov, V. M. (2005), Demography (in Russian), Infra, Moscow.
Murray, J. D. (2002), Mathematical Biology. I. An Introduction, (Third edition), Springer–Verlag, New York, Berlin, Heidelberg.
Preston, S. H., P. Heuveline and M. Guillot (2001), Demography, Measuring and Modeling Population Processes, Blackwell Publishers, Oxford.
Reinshaw, E. (1991), Modelling Biological Populations in Space and Time, Cambridge University Press, Cambridge, doi:10.1017/CBO9780511624094.
Schoen, R. (2007), Dynamic Population Models, Springer, New York.
Venetskii, I. G. (1981), Mathematical Methods in Demography (in Russian), Statistika, Moscow.
Webb, G. F. (1985), Theory of Nonlinear Age-Dependent Population Dynamics, Marcel Dekker, New York.
Received 15 April 2013; accepted 17 April 2013; published 25 April 2013.


Citation: Lushnikov A. A., A. D. Gvishiani, Yu. S. Lyubovtseva, A. A. Makosko (2013), Evolution models for geomedical statistics, Geoinf. Res. Papers, BS1001, doi:10.2205/2013BS008.
Copyright 2013 by the Geophysical Center RAS.